How liquidity provision works
This page describes how liquidity provision works at Charm.
In addition to providing a new model for options trading, Charm's capital efficient architecture also allow LPs to earn high trading fees at much smaller amount of liquidity provision.
Providing LPs at Charm can be lucrative. For the markets that have already settled, LPs earned a total trading fee of $31,670, with a projected APY of 77%. However, this comes with much higher risks.
LPs should therefore read this page in detail, and ensure they fully understand the risks and mitigants, before providing liquidity at Charm.
Before providing liquidity, LPs must be aware of the following risks:
Providing liquidity at Charm is similar to buying a deep in-the-money (ITM) call option - ie the 'safest' call option available at Charm. As such, there is a risk of loosing 100% of your deposits, and you should therefore treated it more as a speculative bet rather than a way to earn a yield.
Depositing and withdrawing funds incurs slippage, which means If you attempt to deposit or withdraw a large amount, you might be overpaying. This slippage is required to prevent economic attacks on the platform.
Liquidity is provided only for the duration of an option market, so LPs will need to withdraw after settlement. In the future, Charm will work on ways to automatically roll liquidity to new markets.
Therefore, if LPs wish to provide liquidity at Charm:
Please provide liquidity in small amounts.
Pay close attention to the price impact indicator.
Consider purchasing a hedging instrument at Charm, if LPs are not comfortable with their exposure. Both the LP's exposure and the recommended hedging instrument will be described in this page.
Our Liquidity provision tutorials provides a step by step guide on how to provide liquidity at Charm.
What is the LP liquidity used for?
The liquidity contributed from LPs are used for the following purposes:
Ensure the AMM will have sufficient funds to meet its payout obligations, regardless of the trading conditions.
Ensure option markets operate with lower slippages throughout the life of the markets.
Before explaining the above, it is helpful to clarify what actually happens when users buys an option. As described in the section on capital efficiency, Charm uses the LMSR (Hanson’s market maker) to provide tokenized spreads that can be combined into various options:
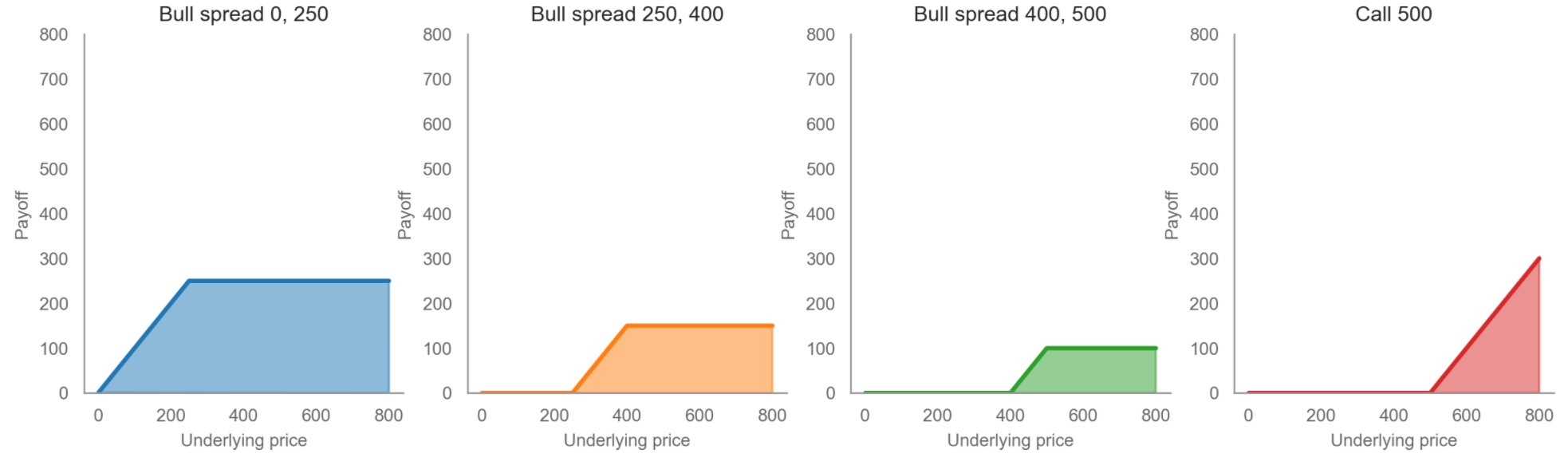
When a user buys an option from the AMM, they’re actually buying the tokenized spreads that make up the option. For example:

The tokenized spreads are represented by 'qi' in the equations below, and the purpose of the LP deposit is to ensure the AMM can fulfil all the payout obligations created by qi, and also to ensure they can be traded at a good level of slippage. This is explained further below:
Purpose 1 - ensuring the AMM can fulfil its payout obligations
The AMM's total payout obligations is represented by:
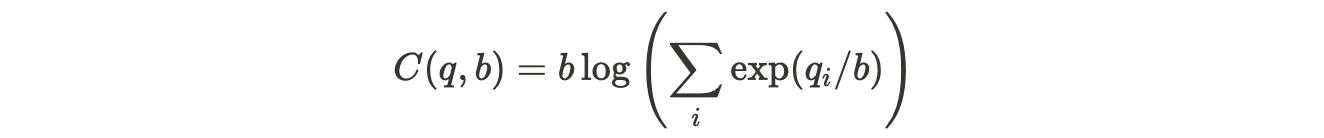
Trading alone will not ensure there are sufficient funds held by the AMM to meet its payout obligations, because even if there are no outstanding options contracts (ie all qi = 0), the AMM is still obliged to pay a certain amount (ie b*log(n)) of money in the worst case scenario. Therefore extra contributions must be made into the AMM that is not related to trading activities, to ensure the AMM can meet all its payout obligations. This extra contribution is the liquidity provided by LPs.
Purpose 2 - Ensuring all qi (and therefore options) can be traded at lower slippages :
The market's slippage level is represented by b. If b is high, it means large trades can occur with lower slippage; and if b is low, it means even small trades would incur high slippage.
For an LP, a high b is preferred because this means larger trades can be placed and therefore more fees can be earned. However to increase b, more funds must be provided by the LP at any given level of open interest* - this is a mathematical property of C(q,b), as exemplified below:
If LPs want to increase b from 10 to 15 when the open interest* is [2, 0, 0], the amount of ETH that needs to be added into the AMM is 5.478 ETH because:
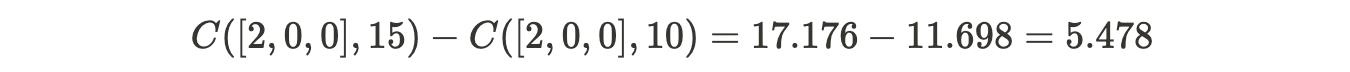
*open interest is the amount of options contracts still outstanding. It is the qi values that feeds into C(q,b) that determines the amount that must be held by the AMM to fulfil all payoff obligations related to these contracts.
After 5.478 ETH have been added, the LP will have 5 LP shares, and b will increased to 15. This means the LP will have 5/15 = 1/3 entitlement of all trading fees generated after they have contributed 5.478 ETH of liquidity. The trading fee earned by LPs will be higher because b is increased, which means larger trades sizes and higher trading fees are possible.
The price of each LP share (ie the price to increase b by 1) increases as more funds are deposited (because b is increased), and as open interest increase (because qi is increased); and decreases as funds are withdrawn or open interest decreases. This means LPs will incur a lot slippage if they deposit large amounts relative to the current pool size, and the amount of slippage will vary for each LPs depending on the trading conditions. Therefore, please pay close attention to the price impact indicator when depositing.
When LPs withdraw funds, b is decreased and slippage will increase. Note there is also slippage when withdrawing and as such, LPs may prefer to wait until after settlement to withdraw their deposits.
What happens to LP deposits after settlement?
After settlement, LPs have to withdraw their funds. The calculation for the withdrawal amount works in a different way from before settlement, and is determined in reference to the total pool value. The total pool value that can be claimed by LPs is calculated by taking the amount held by the AMM (ie C(q,b)) minus the total payoff owed to option holders. Each LP will then receive a cut of the pool value proportional to their LP shares held. For example:
If C(q, b) = 100 ETH with b = 15, and 80 ETH is the total amount owed to holders of the options contracts described in q, then 20 ETH is the net pool value of the pool. If an LP contributed 5 ETH for 5 LP shares, then they will have 5/15 = 1/3 share of the net pool value. This LP can withdraw 1/3 * 20 = 6.67 ETH, for a return of 1.67 ETH or 33% Return In Investment (ROI).
What does LP exposure look like?
The LP exposure can be estimated if we assume the options prices at settlement can be determined with 100% certainty. This is because on settlement, the exact payoff for each option will be known for every possible settlement price. Once the price of each option is determined, it is possible to calculate the number of options that must be bought (ie q) to reach this price.
The graph below simulates the LP payoff (in USDC) on settlement date, for an ETH Calls market with strike prices ranging from 800 to 2240 on settlement date; assuming a constant amount of ETH was deposited at the start of the market.
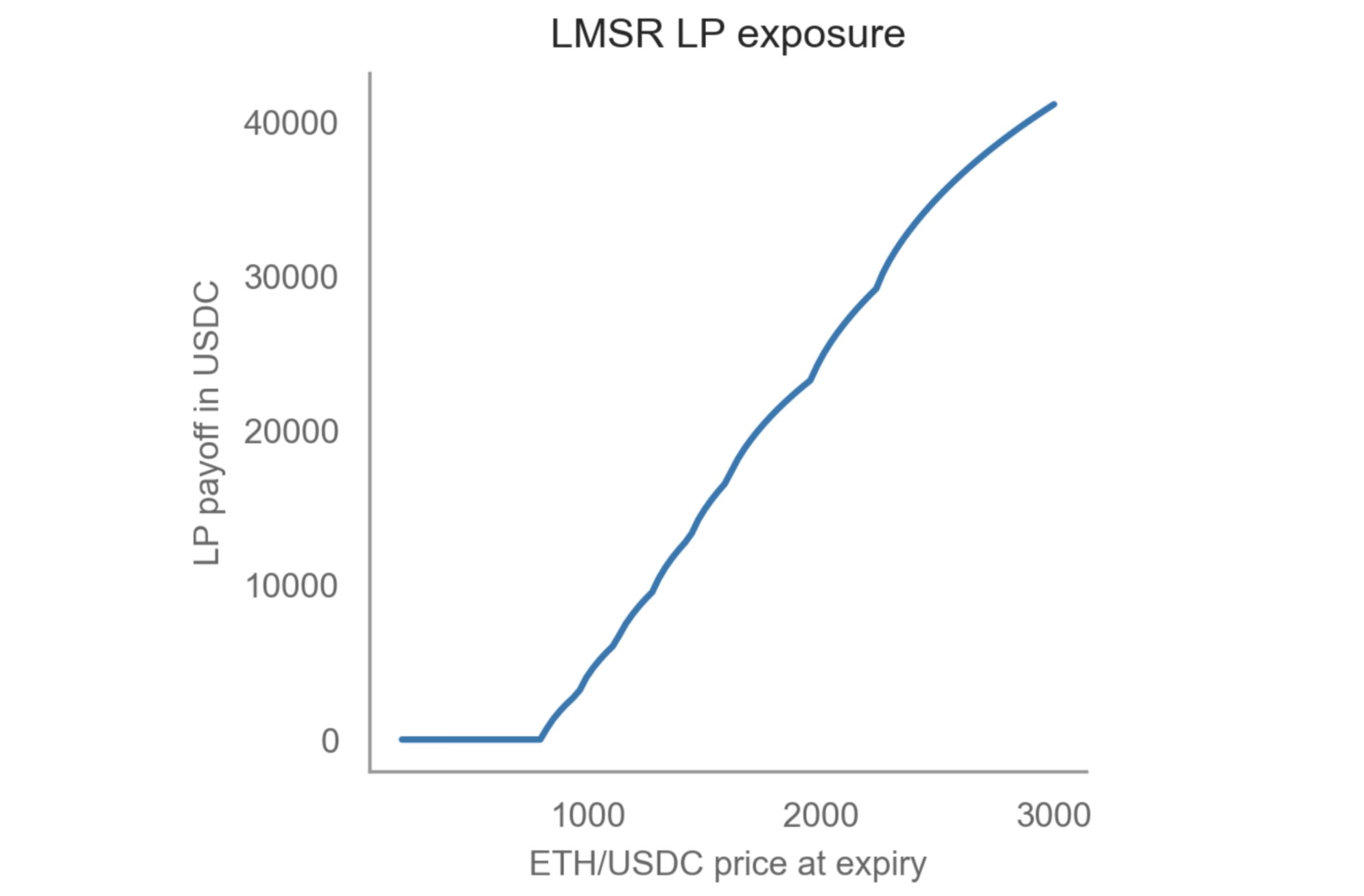
Therefore, the payoff shape roughly resembles a deep in the money call option with the lowest strike price (ie 800 in this case). This means:
LP exposure have the same exposure as buying the 'safest' call option, but 100% loss of capital is still possible if ETH prices fall below the strike strike (eg 800).
Even though the loss is up to 100%, the chances of this happening at Charm is much lower than a constant-product market maker (eg a Balancer pool). This is because 100% loss at Charm will only materialise if the strike price falls below 800, whilst for a constant - product pool, a 100% loss will occur if ANY call option expire worthless. This means there will be 100% to the LPs whenever the ETH price falls below 2240 on settlement date:
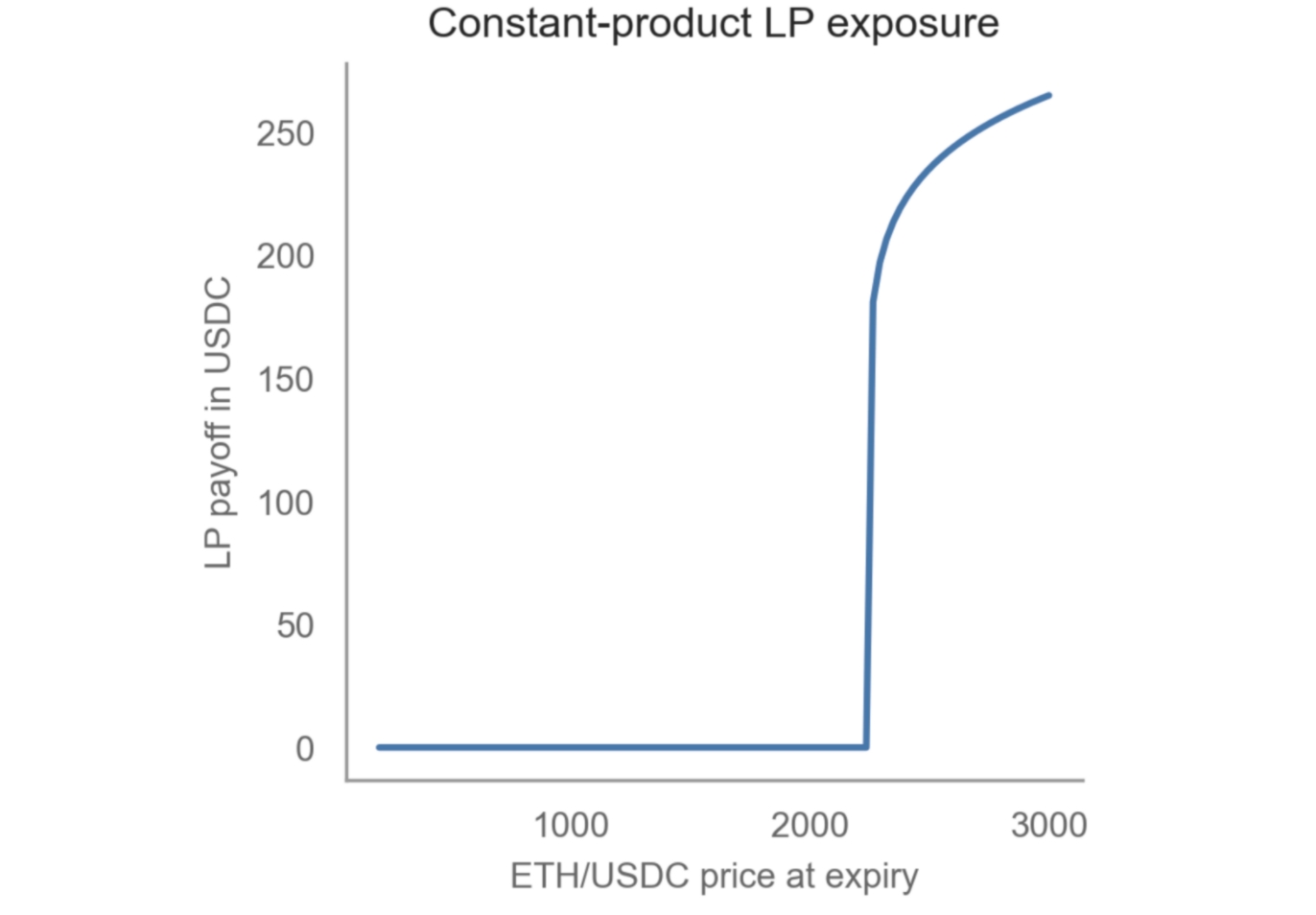
In addition, it’s possible to hedge the LP exposure at Charm by selling the equivalent call at Charm. For example, if a trade is placed to sell calls with Strike Price of 800 immediately after the LP deposit, the exposure will be:

A similar argument to the above can be applied to put markets, except that the LP exposure will be similar to a deep in the money put option with the highest strike price. To hedge this exposure, selling a put option with the highest strike price will need to be purchased at Charm.
The following provide examples of how to LP safely at Charm:
If an LP wish to contribute liquidity to an ETH calls market with strike prices ranging from 800 to 2240, they need to be aware that:
Their exposure will be similar to buying a call option with strike price 800.
They can hedge this exposure by selling a call option with a strike price at 800.
They should pay close attention to the price impact indicator, and ensure they are comfortable with the slippage levels.
It is recommended they hold their LP shares and hedge until after settlement, in order to ensure as much of their risks are reduced as possible.
If an LP wish to contribute liquidity to an ETH puts market with strike prices ranging from 800 to 2240, they need to be aware that:
Their exposure will be similar to buying a put option with strike price 2240.
They can hedge this exposure by selling a put option with a strike price at 2240.
They should pay close attention to the price impact indicator, and ensure they are comfortable with the slippage levels.
It is recommended they hold their LP shares and hedge until after settlement, in order to ensure as much of their risks are reduced as possible.
The strategies above will increase the chances of LPs earning a good yield from the trading fees collected by Charm.
The next pages provides step-by-step instructions on how to trade and LP at Charm.
Last updated
Was this helpful?